BM（Boyer-Moore）字符串搜索算法是一种非常高效的字符串搜索算法。它由Bob Boyer和J Strother Moore设计于1977年。算法对将要搜索的字符串（模式）进行预处理，对文本不进行预处理操作。这个算法适用于模式远短于文本的场景，以及模式会被多次搜索的场景。BM算法在搜索时使用预处理阶段生成的信息以快速跳过文本中不匹配的部分，相比其他很多字符串搜索算法更快。

主要特征

  • 从右向左比较字符。
  • 算法分为两个阶段：预处理阶段和搜索阶段。
  • 预处理阶段时间复杂度空间复杂度均为$O(m+σ)$。$m$是模式长度$σ$是字符集大小，一般考虑为单字节8位共256种。
  • 搜索阶段时间复杂度$O(mn)$。
  • 当模式串是非周期性的，最坏情况下需要做$3n$次字符比较，$n$是文本长度。
  • 最好情况下性能为$O(n/m)$，比如在文本串$b^n$中搜索模式串$a^{m-1}b$，只需要$n/m$次比较。

搜索

基础的匹配算法移动模式串的时候是从左到右，而进行比较的时候也是从左到右的，基本框架是：

1
2
3
4
5
6
7
8
9
10
11
12
j = 0；

while(j <= strlen(text) - strlen(pattern)){
    for (i = 0; i < strlen(pattern) && pattern[i] == text[i + j]; i++);

    if (i == strlen(pattern)) {
        Match(j);
        break;
    }
    else
        j++；
}

BM算法在移动模式串的时候是从左到右，而进行比较的时候是从右到左的，基本框架是：

1
2
3
4
5
6
7
8
9
10
11
12
j = 0；

while（j <= strlen(text) - strlen(pattern)）{
    for (i = strlen(pattern); i >= 0 && pattern[i] == text[i + j]; i--);

    if (i < 0)) {
        Match(j);
        break;
    }
    else
        j += BM()；
}

可以看到，BM算法的核心就是在遇到字符失配时模式串向右滑动的距离。在快速滑动这个思路上BM与KMP是一致的，区别在于滑动的距离具体如何计算。KMP中利用了已经匹配的部分计算滑动距离，并且预先计算成表，使得搜索阶段运行更快。BM中同样利用了已经匹配的部分计算滑动距离，同时还利用了文本中失配字符这一更多的信息，这两种信息的使用就是BM算法的核心。

预处理

BM算法中关于失配后滑动距离的计算包含两个互相独立的方法。

  • 坏字符滑动（bad-character shift）
  • 好后缀滑动（good-suffix shift）

下文中j为文本串中与模式串对齐的首个字符的索引，i为模式串中失配字符的索引。

坏字符

坏字符顾名思义就是失配字符，在这个方法中不考虑坏字符右侧已经匹配的部分，也就是说坏字符出现的模式串的任何位置都无关这个方法的滑动距离计算。

以下图情况为例，t[j+i]位置上的字符'b'与p[i]位置上的字符'a'失配，这时模式串p需要向右滑动以选择一个可能使匹配完成的位置。不考虑失配字符左右的具体内容，由于有t[j+i]位置上的字符'b'存在，模式串p必须滑动到模式串中的字符'b'与文本串中t[j+i]中字符'b'对齐。为了避免遗漏可能的匹配，需要选择p[i]左侧最近的字符'b'。模式串中选择的字符'b'位置为p[k]，则滑动距离为i-k。

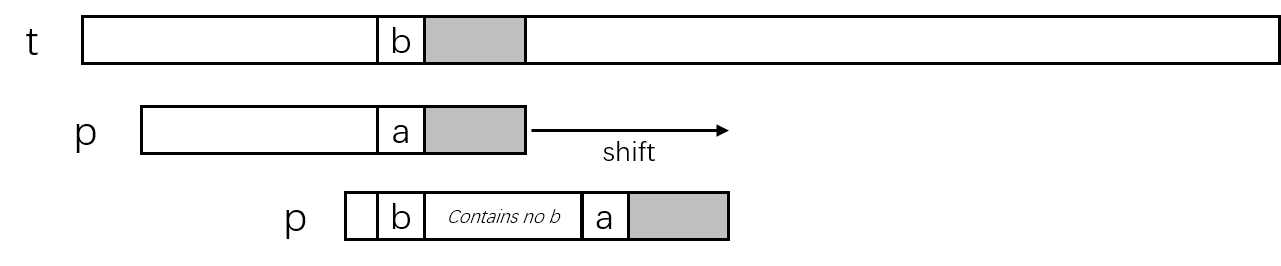
坏字符滑动，失配位置左侧存在字符'b'

如果模式串p中失配字符左侧不存在字符'b'，则将模式串全部移动到文本串中t[j+i]中字符'b'的右侧，这可以看作模式串中选择的字符'b'位置索引为-1，则滑动距离为i+1。

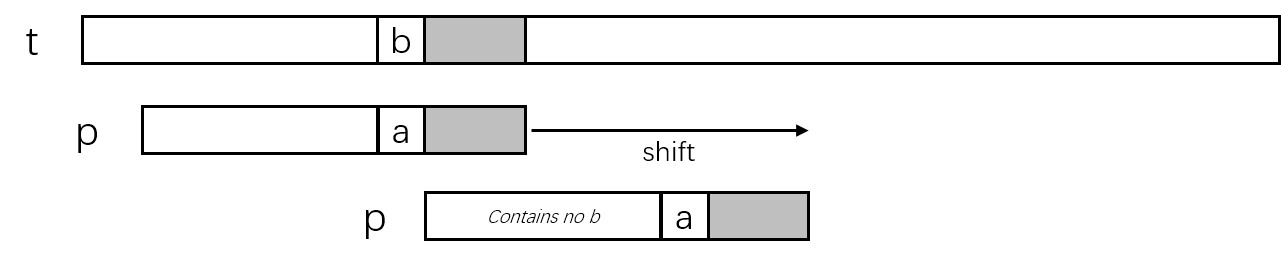
坏字符滑动，失配位置左侧不存在字符'b'

为了满足搜索时任意位置任意字符失配都可以快速查找到该位置左侧最近的失配字符，需要建立一个二维数组，一维长度为模式串长度，一维索引为失配位置，二维长度为字符表（单字节情况可以设为256），二维索引为字符表每个字符。这种二维数组占用空间较大，实际项目中经常采用一维数组存储字符表中每个字符在模式串中最右的位置，这个位置可以记录为距离模式串最右端的距离m-1-i，模式串中未出现的字符记为m。

采用一维数组后，查坏字符表时滑动距离计算为bmBc[text[i + j]] - m + 1 + i，这个值可能是负数。但是由于有并行的好后缀滑动方法存在，最后确定的滑动距离一定是正数。

坏字符表预处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void PreBmBc(const unsigned char *pattern, int m, int bmBc[])
{
    int i;

    for(i = 0; i < 256; i++)
    {
        bmBc[i] = m;
    }

    for(i = 0; i < m - 1; i++)
    {
        bmBc[pattern[i]] = m - 1 - i;
    }
}

好后缀

好后缀就是利用模式串中已经匹配部分的信息计算滑动距离，由于字符比较是由右向左，因此匹配部分是模式的后缀。这个方法中关注匹配的后缀，关注模式串中的失配字符，不关注文本串中的失配字符。

以下图情况为例，已经匹配的好后缀为p[i+1 ... m-1] = t[j+i+1 ... j+m+-1]，好后缀字符串记为u，文本串中的'b'与模式串中的'a'失配。由于已经检查到字符失配，这时模式串p需要向右滑动以选择一个可能使匹配完成完成的位置。考虑到文本串中已经匹配部分的u的存在，移动距离分以下几种情况。

  1. 模式串向右移动，模式串内遇到一串字符可以匹配文本串中的u。同时模式串中新的u前一个字符不能等于模式串中刚刚的那个失配字符，因为如果相等的话肯定不会匹配文本串。
  2. case1中情况没有发生，模式串继续向右移动，模式串的前缀v匹配了文本串中u的后缀。
  3. case1和case2中的情况都没有发生，模式串继续向右移动，直到模式串完全移动到文本串中u的右侧。

这几种情况是按移动距离由短及长排列的。为了避免匹配的遗漏，如果可以对应到移动距离短的情况，就不会再继续移动了，因此这三种情况是有优先级的。下面依次分析。

case 1

模式串内遇到一串字符可以匹配文本串中的u，同时前一个字符不是原失配字符。如果有模式串中有多个位置的串可以匹配，那么选择移动距离最短的，也就是模式串中最右侧的（这个最右不包含后缀u自身）。

在这里u是模式串的后缀，需要检查的模式串内与u相同的串也在模式串内，因此滑动距离可以由模式串自己预处理得到。

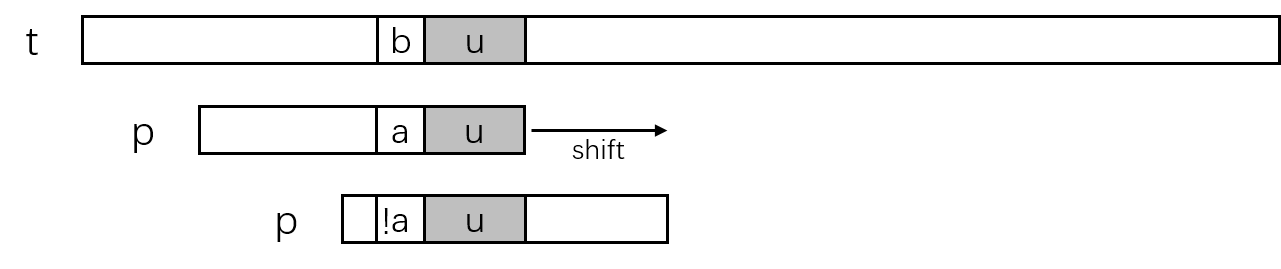
`u`在模式串中间存在

计算case 1

假设存在数组int suff[m]，数组中的每一项suff[i]满足，suff[i]的值为模式串p与模式串前缀p[0 ... i]的最长公共后缀长度。
$ for\ 0 \le i < m, suff[i] = max\{k \ge 0 : x[i-k+1 .. i]=x[m-k .. m-1]\} $

假设存在数组int bmGs[m]，用于存储好后缀滑动距离。

好后缀case 1计算
1
2
3
4
5
6
7
8
9
10
11
12
// 计算每个位置i失配的滑动距离
for (i = 0; i < m; i++) {
    // 已经匹配长度为m-1-i，查找哪个位置的suff[j]等于已经匹配部分的长度。
    // Q:为什么suff数组要记录的是最长公共后缀长度呢？最长的意义是什么？
    // A:这是为了保证前一个字符与刚刚的失配字符不同，或者前一个字符已经位于-1位置(不存在的字符当然与失配字符不同)。
    // j由小到大遍历，为了寻找最右侧符合条件的j，也就是符合条件的j中滑动距离最小的。
    for (j = 0; j < m; j++) {
        if (suff[j] == m - 1 - i) {
            bmGs[i] = m - 1 - j;
        }
    }
}

由于case 1中好后缀滑动距离的填充都是由suff数组计算得到的，而且从上一个计算方法中if (suff[j] == m - 1 - i)这一判断可以看出，suff数组中的每一项值最多会参与一次且一定会参与一次该方法中好后缀滑动距离的计算，因此只要遍历一次suff数组就可以完成case 1的计算。
注意下面遍历过程中赋值的m - 1 - i，由于i是递增的，因此赋值的滑动距离是递减的，最后得到的case 1中的滑动距离都是符合条件且最小。
i最大值取到m-2，因为i取m-1时，bmGs数组索引将取到-1没有意义。而且suff[m-1]的值恒为m，参考上一个计算方法，m-1-i不可能等于m，因此suff[m-1]在case 1计算中没有意义。

好后缀case 1计算改进
1
2
3
for (i = 0; i <= m - 2; i++) {
    bmGs[m - 1 - suff[i]] = m - 1 - i;
}

case 2

模式串的前缀v匹配了u的后缀，这时可能有多个v符合要求，选择最长的哪一个，也就是移动距离最短的。

在这里u是模式串的后缀，v是模式串的前缀，因此滑动距离可以由模式串自己预处理得到。

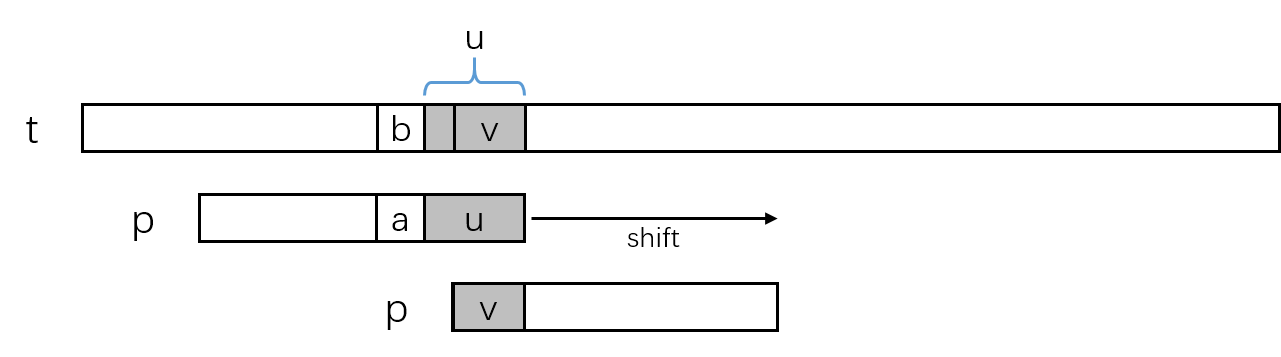
`u`的后缀`v`也是模式串的前缀

计算case 2

suff和bmGs与上面假设相同。

好后缀case 2计算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// i递减，也就是给j留的向右的空间越来越大，配合j保存状态的递增，只扫描模式一次就可以完成计算。
j = 0;
for(i = m - 1; i >= 0; i--)
{
    // 确保以位置索引i结尾的字符串是模式的后缀。
    if(suff[i] == i + 1)
    {
        // j < m - 1 - i，确保j后面至少有i+1长度已经匹配。
        // 为j保存状态，每个bmGs项依次只填充一次。
        // 如果j不保存状态，当i取更小值再次遍历时，m - 1 - i值将会更大，不符合最小滑动距离的要求。
        // 因此bmGs[j]首次取到的值就是符合条件的最小滑动距离。
        for(; j < m - 1 - i; j++)
            bmGs[j] = m - 1 - i;
    }
}

case 3

模式串完全移动到文本串中u的右侧。由于文本串u后的内容没有经过任何匹配检查，因此不能跳过文本串u后的任何内容，模式串最多只能移动到u后的下一个字符位置。

不满足前两种情况时，需要的滑动距离很明显是模式串长度m。

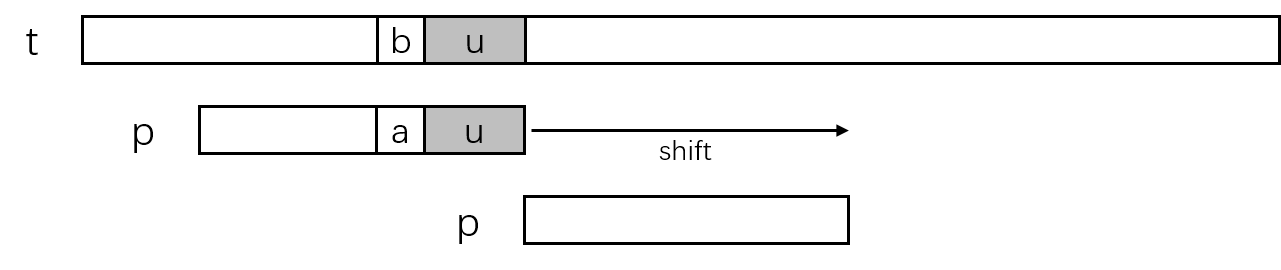
模式串移出文本串

计算case 3

case 3的计算十分简单，由于整体滑动到匹配的内容右侧，因此填充bmGs数组所有项为m。

好后缀case 3计算
1
2
for (i = 0; i < m; i++)
    bmGs[i] = m;

计算suff数组

前面假设了一个suff[m]数组，数组中的每一项suff[i]满足，suff[i]的值为模式串p与模式串前缀p[0 ... i]的最长公共后缀长度。

简单粗暴的计算方式很容易。

suff数组计算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void suffixes(const unsigned char *p, int m, int *suff)
{
    int i, j;
    int k;

    suff[m - 1] = m;

    for(i = m - 2; i >= 0; i--)
    {
        j = i;
        while(j >= 0 && p[j] == p[m - 1 - i + j])
            j--;

        suff[i] = i - j;
    }
}

suff数组有一种改进的计算方式，思路是利用已经计算过的suff项来加速后面的计算。

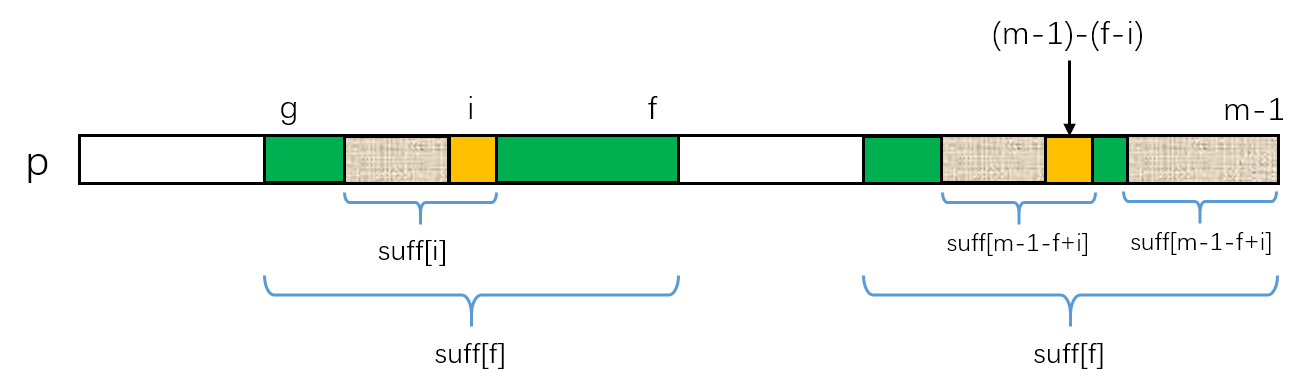
以图为例，f为之前计算过的最长公共后缀的尾部，g为与f匹配的最长公共后缀的首部。
新要计算的位置i一定是在f左侧的。
图中标识suff[f]的两部分内容是相同的，图中标识suff[m-1-f+i]的两部分内容是相同的。
左侧的i相对应的就是右侧的(m-1)-(f-i)。
只要满足suff[m-1-f+i] < i-g（也就是说suff[m-1-f+i]限制在绿色区域内）。由于两块绿色区域内容相同，也就意味着suff[i] = suff[m-1-f+i]。这里的条件必须是小于号，因为如果相等的话，虽然两块标识suff[m-1-f+i]的区域在左侧外部（也就是绿色的外部）失配了，但是两块绿色的左侧外部内容并没有经过检查（也就是说有可能内容相同），这样suff[i]就可能超越出绿色部分（也就是超过i-g），也就无法快速计算了。

suff数组计算改进

suff数组计算改进
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void BoyerMooreSuffixes(const unsigned char *p, int m, int *suff)
{
    int f = 0, g, i;
    suff[m - 1] = m;
    g = m - 1;
    for (i = m - 2; i >= 0; i--) {
        if (i > g && suff[m - 1 - f + i] < i - g)
            suff[i] = suff[m - 1 - f + i];
        else {
            if (i < g)
                g = i;
            f = i;
            while (g >= 0 && p[g] == p[g + m - 1 - f])
                g--;
            suff[i] = f - g;
        }
    }
}

整体代码

BM算法代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
void PreBmBc(const unsigned char *p, int m, int bmBc[])
{
    int i;
    for(i = 0; i < 256; i++)
        bmBc[i] = m;

    for(i = 0; i < m - 1; i++)
        bmBc[p[i]] = m - 1 - i;
}

void BoyerMooreSuffixes(const unsigned char *p, int m, int *suff)
{
    int f = 0, g, i;
    suff[m - 1] = m;
    g = m - 1;
    for (i = m - 2; i >= 0; i--) {
        if (i > g && suff[i + m - 1 - f] < i - g)
            suff[i] = suff[i + m - 1 - f];
        else {
            if (i < g)
                g = i;
            f = i;
            while (g >= 0 && p[g] == p[g + m - 1 - f])
                g--;
            suff[i] = f - g;
        }
    }
}

void PreBmGs(const unsigned char *p, int m, int bmGs[])
{
    int i, j;
    int suff[m];

    BoyerMooreSuffixes(p, m, suff);

    // 三种情况有优先级关系，优先级最高的情况最后填充到表中。
    for(i = 0; i < m; i++)
        bmGs[i] = m;

    j = 0;
    for(i = m - 1; i >= 0; i--)
        if(suff[i] == i + 1)
            for(; j < m - 1 - i; j++)
                bmGs[j] = m - 1 - i;

    for(i = 0; i <= m - 2; i++)
        bmGs[m - 1 - suff[i]] = m - 1 - i;
}
int BMSearch(const unsigned char *p, int m, const unsigned char *t, int n, int *bmBc, int *bmGs) {
    int i, j, m1, m2;

    j = 0;
    while (j <= n - m ) {
        for (i = m - 1; i >= 0 && p[i] == t[i + j]; i--);

        if (i < 0) {
            printf("Match index %d\n", j);
            return j;
        } else {
            j += (m1 = bmGs[i]) > (m2 = bmBc[t[i + j]] - m + 1 + i)? m1: m2;
        }
    }
    return 0;
}

void test(const unsigned char *p, int m, const unsigned char *t, int n) {
    int bmBc[256];
    int bmGs[m];

    PreBmBc(p, m, bmBc);
    PreBmGs(p, m, bmGs);

    BMSearch(p, m, t, n, bmBc, bmGs);
}

int main() {
    char p[] = "example";
    int m = strlen(p);

    char t[] = "here is an example";
    int n = strlen(t);

    printf("pattern %s\n", p);
    printf("text    %s\n", t);

    test((unsigned char *)p, m, (unsigned char *)t, n);

    return 0;
}